２０２３－１２－１５
株式会社　東芝

世界初、計算困難な２次離散最適化に基づく高度な株式取引戦略を
量子インスパイアード計算機「シミュレーテッド分岐マシン」を用いて執行するシステムを実証
－高速リアルタイム取引戦略と資産運用戦略の先駆的事例－

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
概要
当社は、株式市場において多数の銘柄の価格の複雑な関係性を量子インスパイアード最適化計算機「シミュレーテッド分岐マシン（以下、SBM）」（*1-6）を用いて高速に分析し新たな取引機会を検出することを特長とする、高速リアルタイム取引システム2例と、資産運用システム1例を開発し、その執行能力や有効性を実証しました。

金融取引・資産運用戦略において多数の銘柄の関係性もしくは集合的構造を高精度に分析しようとすると、多くの場合計算困難問題に分類される2次離散最適化に定式化されますが（*7,8）、従来の計算機では高速に解くことは困難でした。第1と第2の高速リアルタイム取引システムは、従来は不可能だった2次離散最適化に基づく高度な発注判断の後、注文を発行し、それが高速に価格の変化する株式市場において意図した数量・価格で約定されうることを、東京証券取引所において実証しました。2次離散最適化に基づく発注が、高速に変化する実株式市場で約定し得ることを実証したのは、世界初となります（*9）。第3の例（資産運用システム）では、2次離散最適化に基づき銘柄を選定する資産運用戦略を、SBMの高速求解能力により、これまでになく大規模な銘柄群（約2000銘柄）を対象に長期間（10年）に渡って評価したところ、その戦略が長期的に優れた運用成績を示すことを実証しました。

SBMは高速な求解性能のみならず、リアルタイム、エッジ、もしくはミッションクリティカルと形容されるシステムに組込むことが可能（*4,5）という特徴を有しています。今般の実証事例は、今後、異なる定義のリスク・リターン指標を取り入れた多様な派生のシステムの開発への適用が期待されます。多数の金融商品間の相関に基づく取引機会の検出・執行は、従来流動性に乏しかった銘柄群への流動性の移転プロセスとして、金融取引市場の適正な価格形成機能および流動性の向上に貢献します（*10,11,12）。本技術の成果は、2023年9月18日付、10月23日付、12月12日付（米国東海岸時間）の3通の論文としてIEEE学術論文誌「IEEE Access」に掲載されました（*13,14,15）。 開発の背景
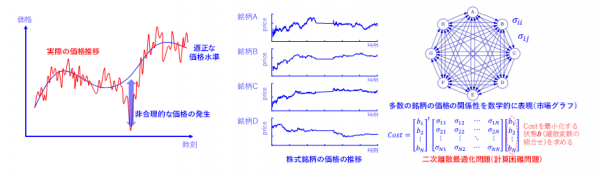
金融取引市場において、適正な価格形成を確保することは、投資家の市場に対する不安感を払拭し、市場の適正な運営を図る上で重要な要素に位置付けられていますが、一時的な需給の不均衡や、市場参加者の心理的なバイアスや集団的な行動によって資産価格が歪められる、いわゆる「非合理な価格」が生じることがあります。株式市場において多数の銘柄の価格の関係性もしくはその集団的ダイナミクスを分析することで、適正価格およびそれを基準にした非合理な価格の発生を推定することが考えられます（*7,8）。相関のある多数の銘柄を分析する問題は、現実的な制約として最小取引単位やその他の離散性を考慮する場合、しばしば2次離散最適化問題に定式化されます（図1）。2次離散最適化問題は計算機理論において計算困難問題に分類され、大規模な問題を高速に解くことは従来困難でした。

当社が量子計算機理論に基づき独自に開発したSBMは、この2次離散最適化問題を高速に解くことを可能とする専用計算機です（*1,2,3）。このSBMを用いて2次離散最適化問題を緩和（線形問題への緩和もしくは連続変数問題への緩和）することなく解く、新しい金融システムが構想されますが、それらは実際の金融市場において、もしくは実際の金融市場データを用いて、実証される必要がありました。


本技術の特徴
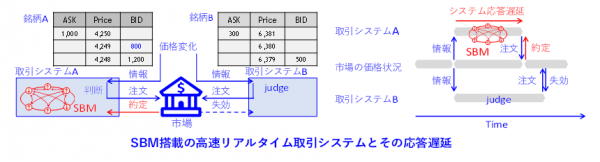
第1と第2の例は、金融分野の代表的な2次離散最適化問題である市場グラフ分析と離散ポートフォリオ最適化に基づく取引戦略を実行するSBM搭載の高速リアルタイム取引システムです。2次離散最適化問題に基づく高度な発注判断の後、注文を発行し、それが高速に価格の変化する株式市場において意図した数量・価格で約定可能な執行能力を有することを実取引により実証したシステムはこれまでありませんでした（図2）。第1と第2のシステムは、東京証券取引所におけるリアルタイム実取引の実績によりその執行能力を、世界で初めて実証しました（*13,14）。

第1と第2のシステムのシステム応答遅延（SBMによる二次離散最適化問題の求解時間のみならず、通信やその他のシステムコンポーネントの遅延をすべて含む）は、33マイクロ秒と164マイクロ秒です（その主要な成分は、二次離散最適化問題の求解時間）。このような短い遅延性能は、（1）SBMの革新的な高速求解能力（*1,2,3）、（2）特定の取引戦略に向けたSBMアルゴリズムとその計算機実装のカスタマイズ（さらなる高速化）（*13,14）、（3）SBMおよび他のシステムコンポーネントのインテグレーション（*13,14）、の3点によって達成されました。

第1と第2のシステムは、取引対象銘柄の最良気配値の更新を通知するパケットを受信する度にSBMを1回以上実行します。実証実験期間において、第1と第2のシステムは典型的には、それぞれ1日あたり100万回以上、500万回以上のSBMによる求解処理を伴う発注判断を実施しました。その期間において、誤動作もしくはそれに基づく誤発注は一度も生じませんでした。


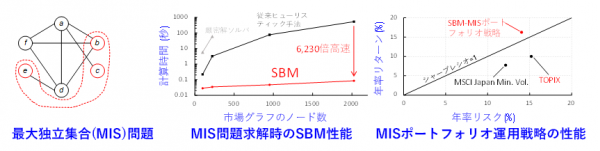
第3の例は、これもまた代表的な2次離散最適化問題である最大独立集合（MIS）問題に基づいて銘柄を選定するポートフォリオ運用戦略の評価システムです（図3）。MIS問題の求解に基づく無相関ポートフォリオが従来提案されていましたが、MIS問題の求解の困難さのためにそのようなポートフォリオ運用戦略の評価は限定的でした（*16,17）。第3の例のシステムは、SBMのMIS問題の高速求解能力より、これまでになく大規模な銘柄群（約2000銘柄）を対象とした長期間（10年）の運用成績の評価を可能としました。このシステムと東京証券取引所のヒストリカルデータを用い、大規模なMISポートフォリオ戦略が長期的に優れた運用成績を示すことを初めて実証しました（*15）。